© 2026 SO-rummet.se
Carl Friedrich Gauss - om den störste matematikern
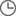

Carl Friedrich Gauss (1777-1855) anses vara en av alla tiders största matematiker. 18 år gammal lyckades han lösa ett matematiskt problem, som varit olöst i 2 000 år. Målning gjord av Christian Albrecht Jensen, 1840.
Någon gång omkring år 1787 gav magister Büttner i Braunschweig sina elever en svår räkneuppgift. Eleverna skulle skriva upp alla tal från 1 till 100 och lägga ihop dem.
Magister Büttner hade en stor klass med omkring 100 elever, och rottingen var ett av hans främsta hjälpmedel när det gällde att hålla ordning. Nu väntade han sig en lugn timme, medan eleverna kämpade med den svåra uppgiften.
Vid denna tid skrev eleverna på griffeltavlor med kritor. Den som först blev färdig med en uppgift lade sin tavla på katedern, och sedan lade de andra sina tavlor på den första allteftersom de blev klara.
Magister Büttner hade nog räknat med att det skulle ta lång tid innan någon av eleverna blev färdig, men han misstog sig. Det hade knappt gått en minut förrän en elev störtade fram och lade sin tavla på katedern.
ANNONS
ANNONS
Den aritmetiska serien
Resten av timmen satt eleven lugnt och väntade, medan hans klasskamrater svettades över sina griffeltavlor. När timmen var slut, kontrollerade magister Büttner tavlan. Där stod endast ett tal, 5050, vilket var helt rätt. De flesta andra hade räknat fel.
Eleven hette Carl Friedrich Gauss (1777-1855), och han förklarade inför sin förbluffade lärare att han insett att räkneproblemet utgjorde en aritmetisk serie. I det här fallet består serien av 50 sifferpar, vars summa alla är 101. 1 + 100 = 101, 99 + 2 = 101 osv. Så fort man inser detta, är det snabbt gjort att räkna ut slutsumman. I exemplet ovan ger serien 50 x 101 = 5050.
Magister Büttner kände naturligtvis till serien, men Gauss hade, tio år gammal, kommit på svaret själv.
Speciell utbildning
Büttner begrep att han inte hade något mer att lära sin elev, köpte en ordentlig lärobok i matematik till honom och lät Gauss specialstudera under lärarassistenten Bartels.
Pojkens snilleblixt blev en vändpunkt i hans liv. Lärarna uppsökte Carl Friedrichs far för att tala om sonens begåvning och hans framtid. Fadern, som arbetat som murare och trädgårdsmästare, var inte helt överens med lärarna.
- Var har ni tänkt få pengar till hans utbildning? undrade fadern.
Lärarna svarade att det säkert skulle gå att finna en rik beskyddare till en så begåvad pojke.
Fadern gick tills vidare med på att låta Carl Friedrich slippa sitt kvällsarbete, som bestod i att spinna en viss mängd lin, och lät honom studera matematik i stället.
Gauss började år 1788 i en högre skola. Hans första matematiska arbete lämnades tillbaka av professorn, som menade att det var onödigt att en så begåvad elev följde undervisningen i en vanlig klass. Gauss fick i stället privatundervisning.
1791 löstes Gauss framtidsproblem. Då fick han träffa hertig Karl Vilhelm av Braunschweig, som blev så imponerad att han gav Gauss pengar till den fortsatta utbildningen.
Det var inledningen till en av världshistoriens största matematiska insatser. Inom matematiken räknas Gauss som jämlike till Arkimedes och Newton.
Klassiska problem
Antikens matematiker tyckte om att ställa upp geometriska problem. Det finns tre klassiska: att konstruera en cirkel med samma yta som en given kvadrat, att konstruera en kub som är dubbelt så stor som en given och att dela en given vinkel i tre lika delar.
För att göra detta får bara två hjälpmedel användas. Det första är linjalen, med vilken det går att rita en rät linje. Den linjal som får användas är inte graderad. Det andra hjälpmedlet är passaren, som förutom att rita cirklar kan användas till att markera lika långa sträckor på en linje, att rita cirkelbågar som skär varandra och ge en punkt som befinner sig på lika långt avstånd från två andra punkter.
ANNONS
ANNONS
Sjuttonhörningen
Det finns även andra problem än de tre klassiska. Ett av dem var att dela en cirkel i 17 lika stora delar. När det är gjort, går det att konstruera en regelbunden sjuttonhörning.
Problemet hade varit olöst i över 2 000 år när Gauss började grubbla på det. En morgon när han, 18 år gammal, låg kvar i sängen under ett lov såg han plötsligt lösningen framför sig.
Gauss lät publicera sin upptäckt i en liten notis i en tidning i juni 1796. Där låter han meddela att han gjort upptäckten och att han inom kort ska lägga fram bevisen för den.
Så gjorde forskare ofta för att vara säkra på att få äran för en viktig upptäckt. Forskningens historia är full av strider mellan olika mer eller mindre framstående vetenskapsmän om vem som egentligen var först.
Gauss var så förtjust över sin upptäckt av 17-hörningens konstruktion att han begärde att få en sådan inhuggen på sin gravsten. Här följde han Arkimedes, som hade räknat ut att om ett klot skrivs in i en cylinder är klotets volym 2/3 av cylinderns. Av alla sina upptäckter var denna en av de Arkimedes var stoltast över. Han sägs därför ha begärt att få ett klot inskrivet i en cylinder inhugget på sin gravsten.
Åsnornas skri
Trots risken att andra skulle ta äran åt sig brydde sig Gauss i fortsättningen inte om att publicera alla sina upptäckter. En anledning var att han ställde enorma krav på de matematiska bevisen för sina teorier. Ett annat skäl var att hans matematiska beräkningar ofta krockade med och kullkastade etablerade begrepp. Den som publicerade sådana teorier kunde räkna med att bli indragen i långa debatter, och det avskydde Gauss. I ett brev talar han om beoternas, alltså åsnornas, skri när något inte passar.
Gauss dagbok upptäcktes först 1898 - 43 år efter hans död, och den har fortfarande inte kunnat tolkas helt. Flera upptäckter beskrivs kortfattat med några kryptiska rader.
Utom i dagboken sparade Gauss sina beräkningar i en stor samling anteckningar. Det tog tio experter 70 år att gå igenom dem och ge ut Gauss samlade arbeten i tolv stora band. Det visade sig att flera matematiska upptäckter som andra forskare gjort långt senare redan gjorts av Gauss som inte brytt sig om att publicera dem.
Fadern och professorn
1807 utnämndes Gauss till professor i astronomi i Göttingen, och där levde han resten av sitt liv. Tjänsten betydde att Gauss i fortsättningen blev oberoende men också att han måste utföra mängder av mätningar som likaväl skulle ha kunnat göras av en mindre begåvad person.
Privat var Gauss kylig och tillbakadragen - det var inte lätt att komma honom in på livet. Han var gift två gånger och fick sammanlagt sex barn.
Trots att Gauss själv beklagat sig över att hans far var hård och tyrannisk i hemmet blev han som far nästan lika hård själv, särskilt mot sina söner.
Hans nära vänner var få, och till de flesta av sina studenter höll Gauss avståndet.
Gauss menade att verkligt begåvade studenter endast behövde en liten vink då och då; de skulle själva finna de matematiska vägarna.
Gauss ogillade att studenterna antecknade under föreläsningen; den som gjorde det kunde han avbryta med orden: - Följ med istället för att skriva.
ANNONS
ANNONS
Fördelningskurvan, påskformeln...
Gauss rön och beräkningar kommer vi fortfarande i kontakt med i vardagslivet.
Gausskurvan, eller normalfördelning som diagrammet också kallas, visar hur ett antal värden fördelar sig runt ett medelvärde, exempelvis elevers kunskaper i matematik.
Gauss fördelningskurva används i många sammanhang. Den beskriver hur ett antal föremål eller företeelser, exempelvis elevers matematikkunskaper, fördelar sig runt ett medelvärde.
Gauss arbetade också med optik och beskrev hur en ny förbättrad lins skulle se ut. Optiska begrepp som brännvidd och huvudplan är resultatet av Gauss arbeten.
En annan känd formel är Gauss påskformel, med vilken det går att beräkna vilket datum påskdagen infaller under vilket år som helst.
Astronomi betydde i många fall ändlösa beräkningar för att få reda på en himlakropps läge. Gauss förbättrade metoden och lade fram ett sätt att beräkna en himlakropps bana som med vissa förändringar används än idag.
Gauss fick också uppdraget att mäta upp och kartlägga det då självständiga kungariket Hannover. Genom detta kunde korrekta kartor framställas. Uppmätningen går till så att området indelas i trianglar, som alla noggrant mäts upp. Alla trianglar läggs sedan samman till en hel karta.
Gauss uppfann även heliotropen. Den används för att fixera hörnen exakt på de trianglar som mäts upp, vilket är av största vikt. Heliotropen använder reflekterat solljus, och den kan användas på flera mils avstånd. Gauss sa sig ha fått idén när han fick en reflex från en fönsterruta i ansiktet.
Triangelns vinkelsumma
När man mäter en triangels vinklar, säger ju en av de grundläggande reglerna i geometrin att summan av vinklarna är 180 grader. Denna regel lades fram redan under antiken av greken Euklides, betraktad som geometrins fader. Men Gauss och flera med honom började undra vad som skulle hända om man antog att det finns trianglar vars vinkelsumma är större, eller mindre, än 180 grader.
En sådan triangel kan t.ex. ritas upp på jordklotet. Om du ritar en rät vinkel vid nordpolen och drar ner de linjer du får till ekvatorn, så ger varje linje en rät vinkel även där. Triangeln har alltså tre vinklar om vardera 90 grader - tillsammans 270 grader. Gauss märkte att de trianglar han mätte upp på jordytan också hade större vinkelsumma än 180 grader. Det beror på att jorden är ett klot. Men eftersom dessa trianglar är mycket mindre än den vi nyss ritade på jordklotet, är också skillnaden mycket mindre - i själva verket så liten att den knappt är märkbar.
ANNONS
ANNONS
Geometri på buktiga ytor
På jordklotet går det att klara sig med den gamla geometrin utan att felen blir alltför stora, men det är annorlunda när det gäller verkligt stora avstånd som de i rymden.
Gauss lade fram ett arbete om geometri på buktiga eller krökta ytor, som så småningom gav Albert Einstein impulser som ledde till den allmänna relativitetsteorin. Där spelar rummets krökning i rymden en stor roll.
"Om inte Gauss hade skapat sin geometri för krökta ytor... är det svårt att föreställa sig att någon annan skulle gjort det", skriver Einstein i en kommentar.
Gauss utförde under sin livstid ensam lika mycket som flera normala forskargrupper gör tillsammans. Men de sista åren sviktade hans tidigare obrutna hälsa, och 1855 dog han, drabbad av hjärtförstoring.
Data och fakta
1777: Carl Friedrich Gauss föds i Braunschweig i nuvarande Tyskland.
1787: Carl Friedrich överraskar med att räkna fram en aritmetisk serie.
1788: Carl Friedrich fortsätter sina studier i en högre skola. Men hans matematiska överbegåvning leder till att han får privatundervisning.
1796: Gauss presenterar sin regelbundna sjuttonhörning.
1807: Gauss blir professor i astronomi i Göttingen. Till Gauss betydelsefulla och bestående insatser hör fördelningskurvan, en kameralins, påskformeln, en kartritningsmetod, en ny metod för att beräkna himlakroppars läge och geometri för krökta ytor.
1855: Gauss avlider.
Uppgifter och frågor
Frågor till texten:
- Hur upptäcktes Gauss matematiska begåvning?
- 18 år gammal kunde Gauss lösa ett matematiskt problem som varit olöst i över 2 000 år. Vilket?
- Hur påverkar Gauss matematiska arbeten din vardag?
- Vilket instrument uppfann Gauss för att underlätta uppmätning av landområden?
- Hur används instrumentet?
- Ge exempel på att reglerna för den geometri för krökta ytor Gauss lade grunden till skiljer sig från reglerna för geometri för plana ytor.
- Lägg ihop talen mellan 101 och 200 genom att använda samma metod för geometriska serier som den unge Gauss gjorde.
M LÄS MER: Vetenskapspersoner och vetenskapshistoria
M LÄS MER: Vetenskap, teknik och kommunikationer 1776-1914
Skrolla ner till listorna med bilder så hittar du mer liknande material.
Litteratur:
Isaac Asimov, Lägg till en dimension, Rabén & Sjögren, 1967
Daniel J Boorstein, The Discoverers, Random House, 1983
Rom Harré, Great Scientific Experiments, Oxford University Press, 1983
Roy Porter (red.), Man Masters Nature, BBC Books, 1987
David Eliot Brody och Arnold R Brody, Upptäckterna som förändrade världen och människorna bakom dem, Wahlström & Widstrand, 1999
John McLeish och Jan Wahlén, Matematikens kulturhistoria, Bokförlaget Forum, 1996
FÖRFATTARE
Text: Kaj Hildingson, journalist och läromedelsförfattare
© 2026 SO-rummet.se















































