Arkimedes - antikens store matematiker och fysiker
En naken vetenskapsman som springer hemåt jublande av lycka är en ganska ovanlig syn. Men invånarna i Syrakusa på Sicilien sägs för över 2 000 år sedan ha fått se just detta. Den glade vetenskapsmannen hette Arkimedes och hade just funnit lösningen på ett svårt problem genom att spilla ut vatten i ett badhus. Det kan hända att den här historien inte är sann. Däremot är det sant att Arkimedes räknas som en av historiens största matematiker och uppfinnare. Än idag arbetar forskare med att tyda några av hans skrifter, skrifter som antogs vara förlorade för alltid men som återfanns i en möglig bok som såldes på auktion i slutet av 1990-talet.
Arkimedes (ca 285 f.Kr-212 f.Kr) på en målning av Domenico Fetti, 1620.
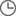
När kung Hiero II av Syrakusa på Sicilien en dag för över 2 000 år sedan fick sin nya guldkrona, blev han misstänksam. Hade guldsmeden verkligen använt allt guld denne hade fått till kronan? Kanske hade guldsmeden tagit en del guld själv och blandat upp guldet med någon annan metall?
Kungen visste hur mycket det guld vägde som guldsmeden fått, och kronan vägde lika mycket, men kungen var ändå tveksam.
En möjlighet att få reda på sanningen var att smälta ner kronan. Men kung Hiero ville inte förstöra det vackra arbetet. Kronan kunde ju vara av rent guld. Till sist bad kungen sin vän Arkimedes (ca 285 f.Kr-212 f.Kr) om hjälp. Han hade rykte om sig att vara den intelligentaste mannen i Syrakusa.
ANNONS
Data och fakta
Ca 285 f.Kr: Arkimedes föds i Syrakusa på Sicilien. Bland hans uppfinningar och upptäckter märks: Arkimedes princip, skruv och hävstångslagar. Beräkningen av klotets yta och volym. Beräkningen av ett bra värde på pi.
212 f.Kr: Arkimedes dör under romarnas stormning av Syrakusa.
Kronan, vattnet och volymen
Arkimedes fick kronan och började fundera. Han kom på att det skulle gå att utnyttja det faktum att olika ämnen med samma volym har olika vikt.
Ett föremåls volym är den plats det upptar. En kub där varje sida är en centimeter har en volym på en kubikcentimeter. Men olika ämnen med samma volym väger olika mycket. Exempelvis väger en kubikcentimeter guld mer än en kubikcentimeter silver.
Vikt och volym hänger alltså ihop. Två guldföremål som väger exakt lika mycket har samma volym, även om de har olika form. En kubikcentimeter guld och ett guldhalsband har samma volym, om de väger lika mycket.
Arkimedes lånade ett stycke guld av kungen - många kungar hade gott om guld på den tiden - som vägde exakt lika mycket som kronan. Om guldstyckets volym och kronans volym var lika stora, skulle alltså kronan vara av rent guld. Guldstyckets volym var lätt att beräkna, men hur skulle det gå till att beräkna volymen på något så oregelbundet som en kungakrona?
Enligt vad som berättas gick Arkimedes grubblande till stadens badhus. Där klev han ner i ett fullt badkar, vattnet rann ut över sidorna, och i en blink hade Arkimedes löst gåtan.
- Heureka (Jag har funnit det), lär han ha ropat och rusade iväg - så upphetsad att han glömde kläderna och sprang hem naken genom gatorna.
Arkimedes hade insett att volymen av det vatten som rann från karet var lika stor som volymen av hans egen kropp. Om han sänkte ner kronan i ett fullt kar med vatten, samlade upp det vatten som rann ut och mätte dess volym, skulle han ha kronans volym.
Arkimedes sänkte ner kronan och mätte det utrunna vattnets volym. Guldkronans volym stämde inte med dess vikt. Det bevisade att guldet blandats upp med en annan metall. Guldsmeden hade försökt lura kungen!
Detta är bara en av flera historier om Arkimedes, antikens störste matematiker och ansedd som ett av de största genierna genom tiderna. Historierna om Arkimedes speglar det väldiga intryck hans uppfinningar och upptäckter gjorde. Inte om någon annan av antikens vetenskapsmän finns lika många berättelser.
Moderna historiker är tveksamma till historien om Arkimedes och guldsmeden. Inte heller är det säkert att han ropade Heureka. Det finns inga uppgifter om detta i Arkimedes egna skrifter. Men uttrycket Heureka har i sin engelska form Eureka levt kvar och dyker upp då och då i filmer och böcker.
ANNONS
ANNONS
Uppfinningar och upptäckter
Arkimedes skruv har använts för konstbevattning in i vår tid. Uppfinningen består av en skruv som vrids inne i en cylinder. När skruven doppas i vatten och vrids runt, lyfts vatten upp och rinner ut genom övre änden. För att Arkimedes skruv ska fungera måste den vara placerad lutande.
Arkimedes levde större delen av sitt liv i Syrakusa på Sicilien och var både uppfinnare och matematiker. Han anses ha uppfunnit Arkimedes skruv, som har använts för konstbevattning in i våra dagar. Anordningen består av en ihålig skruv som vrids inne i en cylinder. När skruvens nedre ända sänks i vatten och skruven vrids, lyfts vattnet upp allt högre och högre till det rinner ut i övre änden.
Arkimedes var den förste som på allvar studerade vattnets lyftkraft och hävstångslagen.
Han har gett namn åt Arkimedes princip, som innebär att föremål som placeras i vätska tycks förlora lika mycket i vikt som den vätska föremålet tränger undan väger. Denna princip används ännu idag för att beräkna vikten på fartyg.
Att det med hjälp av en hävstång gick lätt att flytta tunga föremål var känt sedan tidigare, men det var Arkimedes som sammanställde hävstångslagarna. Han införde också begreppet tyngdpunkt.
- Ge mig en fast punkt, och jag ska rubba jorden, sägs han triumferande ha sagt sedan han upptäckt vilka krafter en hävstång kunde ge människan.
De moderna historikerna förnekar att Arkimedes gjort detta uttalande.
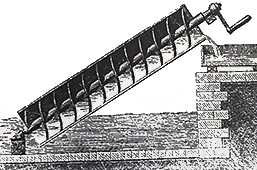
Bild: SO-rummet.se Om vridpunkten på en hävstång ligger mitt på stången, är den kraft som behövs för att lyfta en tyngd lika stor som tyngden. Men flyttas vridpunkten så att ena hävarmen blir lång och den andra kort, kan en liten kraft på den långa armen lyfta en stor tyngd på den korta. Hävstången är ett av människans äldsta mekaniska hjälpmedel; med den kan enkelt tunga saker lyftas.
ANNONS
Värdet på pi
En av Arkimedes stora bedrifter var att beräkna ett bra värde på pi. Pi är kvoten mellan längden av en cirkels omkrets och längden av dess diameter. Detta förhållande är detsamma i alla cirklar.
Ett bra värde på pi är viktigt inom många områden, exempelvis för att beräkna ytan eller arean av en cirkel. Pi används också bland annat för att beräkna volymen av cylindrar och volymen och ytan av klot.
Omkrets = diameter x pi
Pi är ett irrationellt tal, alltså ett tal med ett oändligt antal decimaler. När omkretsen och diametern divideras, går divisionen alltså aldrig jämt upp. Idag används värdet 3,141592...
För att bestämma ett värde på pi går det att rita upp en cirkel och bestämma att diametern i den är ”en enhet". I så fall blir ju pi detsamma som omkretsens längd, eftersom omkretsen dividerad med 1 är omkretsen själv. Problemet blir då att bestämma omkretsens längd. Ju bättre värde på omkretsens längd, desto bättre värde på pi.
Arkimedes gjorde så att han lät en triangel inskrivas i cirkel med diametern ”en enhet”. Utanför cirkeln omskrev han en annan triangel. Trianglarnas omkrets var lätta att beräkna. Den inre triangelns omkrets måste vara mindre än cirkelns och den yttre större.
Genom att förändra trianglarna till sexhörningar kom Arkimedes närmare ett exakt mått på cirkelns omkrets. Sexhörningarnas och andra månghörningars omkrets går att beräkna. Ju fler hörn en månghörning har desto närmare kommer den cirkelns form och desto bättre värde ger månghörningens omkrets på pi.
Arkimedes hade tålamod och tid nog att arbeta med nittiosexhörningar och kunde visa att pi låg mellan 3 10/71 och 3 1/7. Värdet är mycket bra, och ett bättre skulle räknas fram först på 1500-talet.
Arkimedes berättade om sina upptäckter redogjorde i brev till kollegor. Några av breven har skrivits av genom tiderna. Därför har en del av Arkimedes beskrivningar bevarats till vår tid.
Det finns också avskrifter av verk bevarade som anses skrivna av Arkimedes själv.
I dessa avskrifter finns bland annat formlerna för beräkning av klotets yta (4 pi r2) och dess volym (4/3 x pi r3). Arkimedes hade också räknat ut att om ett klot skrivs in i en cylinder är klotets volym 2/3 av cylinderns.
Av alla sina upptäckter var Arkimedes stoltast över dessa och han begärde att få ett klot inskrivet i en cylinder inhugget på sin gravsten. År 75 f.Kr. återfanns verkligen en sådan sten på Sicilien men den tappades bort och har aldrig hittats igen.
ANNONS
Sandräknaren
Arkimedes använde det grekiska siffersystemet. Det påminner om det romerska och var avsevärt krångligare att använda än de system vi använder i dag. Hans matematiska insatser blir därmed ännu större.
Arkimedes insåg själv hur klumpigt det grekiska systemet var. I sin skrift Sandräknaren beräknar han hur många sandkorn det skulle gå åt för att fylla hela det då kända universum. Arkimedes kommer fram till att det räcker med 10 upphöjt till 63 sandkorn för att fylla universum. Utskrivet på vanligt sätt är talet en etta följt av 63 nollor.
Skriften har väckt både matematikers och historikers intresse. Dels konstruerar Arkimedes där ett helt nytt talsystem, dels ger boken fängslande upplysningar om revolutionerande idéer som astronomen Aristarkos lagt fram.
Enligt honom roterade jorden runt solen och roterade dessutom ett varv runt sin egen axel på ett dygn: Aristarkos menade också att planeterna rörde sig runt solen. Han är sannolikt den förste som har lagt fram denna teori, som naturligtvis omgående möttes av massiv kritik. Teorin lades därför åt sidan under 2 000 år tills Nicolaus Copernicus lade fram samma tankegång på 1500-talet.
”Rubba inte mina cirklar”
Historierna om Arkimedes är många, och till och med hans död har blivit legendarisk.
Arkimedes hemstad Syrakusa belägrades av romarna under den romerske generalen Marcellus. Åter kom Arkimedes sin härskare till hjälp och konstruerade så effektiva krigsmaskiner att romarna tvingades dra sig tillbaka. Ett av dessa vapen var en katapult.
Ett annat vapen ska ha varit en serie speglar som fångade upp solljuset, koncentrerade det i en stråle och sände strålen mot romarnas fartyg som sattes i brand. Om denna uppfinning har existerat annat än som idé är dock högst osäkert. Moderna försök med att bygga sådana speglar har visat att taktiken skulle kunna ha fungerat, om nu speglarna någonsin blev byggda.
Till sist stormade romarna ändå Syrakusa. Marcellus hade gett order om att Arkimedes skulle tas levande. Men när de romerska soldaterna stormade in i hans hus, satt Arkimedes och grubblade över en figur han ritat på en sandtäckt bricka. Han vägrade uppge sitt namn och ropade:
- Rubba inte mina cirklar! Då högg soldaterna ned honom.
De moderna historikerna förstör även denna goda historia. De påpekar nyktert att det enda vi med säkerhet vet är att Arkimedes dog under stormningen av Syrakusa.
Arkimedes verk glömdes bort i Europa under lång tid och studerades endast av arabiska matematiker. Först på 1500- och 1600-talen började hans verk studeras igen i Europa.
ANNONS
ANNONS
En del av Arkimedes skrifter har varit borta ännu längre. Det viktiga verket Om mekaniska teorem återupptäckte först sent på 1800-talet.
1998 såldes en mögelskadad grekisk bönbok med sidor av pergament på auktion i New York. Boken var en så kallad palimpsest, alltså en skrift där den ursprungliga texten skrapats bort och ersatts med en ny. Det var vanligt att göra så eftersom pergament, som är gjort av skinn var dyrbart. Till den bönbok som såldes i New York hade det gått åt 24 fårskinn. Texter som ansågs värdelösa skrapades därför bort och ersattes med nya.
Att bönboken innehöll bortskrapad text från Arkimedes böcker var känt sedan tidigare. Med modern teknik kunde forskare avslöja att boken innehöll långt fler avskrifter av Arkimedes texter än som tidigare var känt. En del av dessa texter var bara kända genom sina titlar och hade ansetts förlorade för alltid. Texterna visar också att Arkimedes hade gjort flera matematiska upptäckter än som tidigare var känt.
Varför hoppade Arkimedes, enligt en historia, en dag upp ur ett kar i badhuset och rusade hem utan att ta på sig sina kläder?
Vid samma tillfälle ska han ha yttrat ett ord som sedan blev berömt. Vilket?
På vilken ö i Medelhavet levde Arkimedes större delen av sitt liv?
Nämn några av Arkimedes viktigaste matematiska upptäckter.
Vilka var enligt legenden Arkimedes sista ord, och varför yttrade dem?
Hur bar sig Arkimedes åt för att få fram ett bra värde på pi?
Vilka är de två anledningarna till att boken Sandräknaren väckt matematikers och historikers intresse?
Förklara hur Arkimedes skruv fungerar.
Du får i din hand två små statyer. Båda väger ett halvt hekto, och de ser för ögat likadana ut. Men du vet att en staty är av rent guld och att en är en förfalskning. Förklara hur du med hjälp av Arkimedes upptäckter avgör vilken staty som är av guld.
Litteratur: Roy Porter (red.), Man Masters Nature, BBC Books, 1987 John McLeish och Jan Wahlén, Matematikens kulturhistoria, Bokförlaget Forum, 1996 Staffan Hansson, Teknikhistoria - en historia om tekniskt kunnande och dess betydelse för individ och samhälle från äldsta tid fram till 1900-talet, Studentlitteratur, 1990 Henry Hodges, Technology in the Ancient World, Penguin, 1971 Daniel J Boorstein, The Discoverers, Random House, 1983 Rom Harré, Great Scientific Experiments, Oxford University Press, 1983 Gordon Taylor m.fl., Uppfinningarnas historia, Det bästa, 1985
FÖRFATTARE
Text: Kaj Hildingson, journalist och läromedelsförfattare
I fokus första avsnitt handlar om atensk demokrati. Julia, Mattias och Kristoffer pratar om vad ordet demokrati betyder och hur den atenska demokratin fungerade. Var det verkligen demokrati i antikens Aten?
